![[gif goes here]](int.gif) ), underlines, and
superscripts and subscripts, so it requires
Netscape 3, Explorer 2, or later browsers.
), underlines, and
superscripts and subscripts, so it requires
Netscape 3, Explorer 2, or later browsers.
Browser requirements. This web page uses gif images
(![[gif goes here]](int.gif) ), underlines, and
superscripts and subscripts, so it requires
Netscape 3, Explorer 2, or later browsers.
), underlines, and
superscripts and subscripts, so it requires
Netscape 3, Explorer 2, or later browsers.
Still later, Riemann refined the definition that Cauchy had been using, and investigated the integrals of discontinuous functions. The Riemann integral is simpler to define than any of the other integrals discussed below, and it is the "standard" integral that we teach to undergraduate students. Still, it is more complicated than the antiderivative, and it seems to be beyond the understanding of many undergraduate students.
The theory of the Riemann integral was not fully satisfactory. Many important functions do not have a Riemann integral -- even after we extend the class of integrable functions slightly by allowing "improper" Riemann integrals. Moreover, even for integrable functions, it is difficult to prove good convergence theorems using only the tools ordinarily associated with Riemann integrals. A pointwise, bounded limit of Riemann integrable functions is not necessarily Riemann integrable. (For instance, since the rationals are enumerable, the characteristic function of the rationals can be represented as the pointwise limit of a sequence of characteristic functions of finite sets.)
In 1902, Henri Lebesgue devised a new approach to integration, overcoming many of the defects of the Riemann integral. Lebesgue's definition is appreciably more complicated, but Lebesgue's techniques yield better convergence theorems and, for the most part, more integrable functions. The Lebesgue integral has become the "standard" integral in our graduate courses in analysis.
The Lebesgue integral is strictly more general than the proper Riemann integral -- i.e., it can integrate a wider class of functions. However, in comparing the improper Riemann integral with the Lebesgue integral, we find that neither is strictly more general than the other. Examples will be given later in this article.
Neither the improper Riemann integral nor the Lebesgue integral yielded a fully satisfactory construction of antiderivatives. Slightly more satisfactory answers -- i.e., more general notions of integral -- were given by Arnaud Denjoy (1912) and Oskar Perron (1914). Denjoy's and Perron's definitions turned out to be equivalent; both were very complicated.
Decades later, independently, Ralph Henstock (1955) and Jaroslav Kurzweil (1957) found a much simpler formulation of the Denjoy-Perron integral. In fact, the Henstock-Kurzweil formulation -- the gauge integral -- is considerably simpler than the Lebesgue idea, and its definition is only slightly different from the definition of the Riemann integral. Consequently, interest in this integral has been rising over the last few decades, and some mathematicians have even advocated that we should teach the gauge integral either alongside or in place of either the Riemann integral or the Lebesgue integral. I will express my own opinions about that possibility, at the bottom of this web page. (In January 1997 I circulated a letter advocating the use of the gauge integral. It was signed by Henstock, Kurzweil, and several other leaders of the gauge integral movement. I distributed it to several publishers of calculus textbooks. However, it apparently hasn't had any effect.)
Henstock, Kurzweil, and other early researchers in this area were writing in rather specialized and technical terms for advanced audiences, so their ideas did not spread quickly at first. Here is a partial bibliography:
Now a very slight modification yields the definition of the gauge integral. Again, there are several different, equivalent ways to define the gauge integral; we shall give only the formulation which emphasizes the similarity between the Riemann and gauge integrals.
The only change is in the use of delta. Instead of a positive constant, delta must be a positive-valued function. The function delta is called a gauge. It doesn't have to be continuous, or measurable, or anything else; it just has to take strictly positive values. Also note that
en español
![[gif condition is replaced]](replaced.gif)
The collection of numbers n, si, ti is called a tagged division (or a tagged partition); the numbers si are called the tags. The tagged division is called δ-fine if it satisfies the condition ti-ti-1 < δ(si) for all i. Some of the books and papers on this subject use a slightly different condition, e.g., that si-δ(si) < ti-1 < ti < si+δ(si). This affects the development of the theory only superficially -- e.g., in some places we need to replace an ε with either 2ε or ε/2.
Cousin's Lemma states that for any gauge δ, there exists at least one δ-fine tagged division. Cousin's Lemma is not obvious; that is admittedly a drawback in the gauge theory. The proof of Cousin's Lemma uses the fact that the real number system has the Least Upper Bound property.
There are several slightly different ways to prove Cousin's Lemma; here is a sketch of one of the proofs. Let S={x∈[a,b] : there exists a δ-fine tagged division on [a,x]}. Then S is nonempty, since a∈S. Also, S is bounded above by b. By the Least Upper Bound Property, the set S has a supremum, or least upper bound; let us denote that number by σ. Then σ∈[a,b]. If σ < b, use the fact that δ(σ) > 0 to arrive at a contradiction. If σ = b, use the fact that δ(b) > 0 to prove that the supremum is actually a maximum -- i.e., that b is a member of S.
The set of all gauge-integrable functions from [a,b] to R is a vector space -- i.e., any constant multiple of such a function or any sum of two such functions is another such function. That vector space is often known as the Denjoy space, because of some work Denjoy did in studying it.
We have only considered the simplest possible versions of the definitions, but we remark that some generalizations are possible.
However, the fact that we're using properties of intervals means that the gauge integral does not generalize readily to settings other than intervals. It can be generalized to functions defined on the whole real line, or to functions defined on finite-dimensional spaces, but its definition and theory then become slightly more complicated. It apparently can also be generalized to infinite dimensional spaces, and more abstract setttings, but I'm not very familiar with this theory, and I believe it's a lot more complicated. Some of Henstock's writing deals with this theory. I believe that Muldowney's book gives a more elementary treatment of this theory, but I have to confess that I'm not very familiar with the theory or with his book.
Contrast that with the Lebesgue approach, which requires far more prerequisite equipment (sigma-algebras, measures, measurable sets, measurable functions) but then generalizes without any difficulty at all to settings entirely unrelated to intervals. Thus, the Lebesgue approach may be preferable if one wants to study stochastic processes such as Brownian motion. (Brownian motion can be explained in terms of Wiener measure, a measure on an infinite-dimensional space of continuous functions.)
Here is an example of the concreteness of the gauge integral: Any introductory course on measure and integration should include a construction of Lebesgue measure, but how should that be done? The usual constructions are rather complicated and abstract; they have little to do with the uses of Lebesgue measure. But it is easy to define the gauge integral, and after we've defined it we can proceed this way: Define
![[gif define measure]](measure.gif)
![[gif simple example]](example.gif)
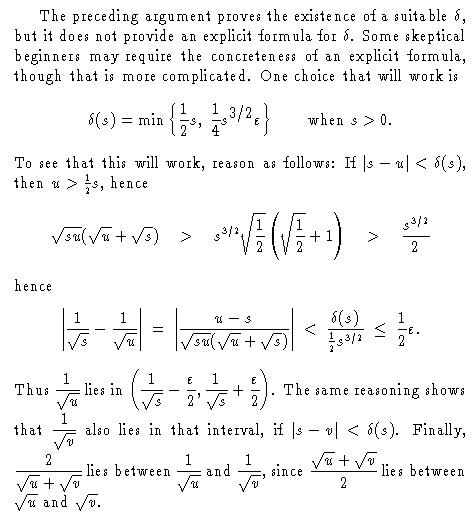
![[gif image of Venn diagram]](venn.gif)
As indicated by the Venn diagram above, not every Lebesgue integral can be viewed as a Riemann integral, or even as an improper Riemann integral. For a simple example, consider the characteristic function of the rationals.
As indicated by the Venn diagram above, not every improper Riemann
integral is a Lebesgue integral. For an example, let f(t) =
t2 cos(1/t2) with f(0)=0. Then
![[gif integral]](int.gif) 01|f '(t)|dt
is infinite, and the Lebesgue integral
01|f '(t)|dt
is infinite, and the Lebesgue integral
![[gif integral]](int.gif) 01f '(t)dt
does not exist, but the improper Riemann integral
01f '(t)dt
does not exist, but the improper Riemann integral
![[gif integral]](int.gif) 0Tf '(t)dt exists (for
any T) and equals f(T).
0Tf '(t)dt exists (for
any T) and equals f(T).
The examples above are typical. If g(t) is any gauge
integrable function on [a,b], then g(t) is Lebesgue
measurable. Hence the Lebesgue integral ![[gif
integral]](int.gif) ab|g(t)|dt exists, if we
permit infinity as a possible value. The Lebesgue
integral
ab|g(t)|dt exists, if we
permit infinity as a possible value. The Lebesgue
integral ![[gif
integral]](int.gif) abg(t)dt exists (with
its usual definition) if and only if
abg(t)dt exists (with
its usual definition) if and only if ![[gif integral]](int.gif) ab|g(t)|dt is
finite. For any nonnegative function, the Lebesgue and
gauge integrals are the same.
ab|g(t)|dt is
finite. For any nonnegative function, the Lebesgue and
gauge integrals are the same.
This analogy may be helpful: The gauge integrable functions are like convergent series; then the Lebesgue integrable functions are like absolutely convergent series. The absolutely convergent series are easier to work with, and yield a tidier theory. The convergent series are more general, but only occasionally do we need to work with a series that is conditionally convergent.
Rapidly oscillating functions such as the derivative of t2 cos(1/t2) are the only ones added to our collection of integrable functions when we switch from the Lebesgue integral to the gauge integral. These functions are more often used for pathological counterexamples than for positive applications. Thus the greater generality of the gauge theory does not make it much more applicable. (A possible exception is in the theory of differential equations; there seem to be some important new applications there.) For the most part, the big advantage of the gauge integral is the new insight that it yields into the Lebesgue integral.
Here is another drawback to the gauge theory: The Lebesgue theory yields the Banach space L1[a,b] of all Lebesgue-integrable functions. It's a very nice space, with a nice metric and nice convergence theorems. The gauge theory yields a slightly larger vector space, which we might call G[a,b]. But the metric and the convergence theorems for this space are much less nice. That's not surprising: this space contains not only the nice functions of L1[a,b], but also some additional functions that are rather nasty. If we don't really need to work with those nasty functions, we might prefer to stick to the setting of L1[a,b], which has nicer worktools (i.e., the metric, the convergence theorems, etc.).
Result (a), or one like it, is what we teach our graduate students, under the stronger assumption that f is Lebesgue integrable. Result (b), or one like it, is what we teach our undergraduates -- usually under the assumption that f is continuous throughout all of [a,b], but that stronger assumption is not really needed.
First Fundamental Theorem of Calculus (derivatives of integrals). Let f be a real-valued, gauge integrable function on [a,b], and let F(t) = atf(s)ds. Then:
- (a)
- the derivative F '(t) exists and equals f(t), for almost every t in [a,b].
- (b)
- the derivative F '(t) exists and equals f(t), at each t where f is continuous.
We teach our undergraduates a theorem like this, but it usually has the additional hypothesis that the Riemann integral
Second Fundamental Theorem of Calculus (integrals of derivatives). Let F be a real-valued, differentiable function on [a,b]. Then the gauge integral ab F '(t)dt exists and equals F(b)–F(a).
![[gif integral]](int.gif) ab F '(t)dt
exists. That is a conclusion, rather than a
hypothesis,
if we use the gauge integral.
ab F '(t)dt
exists. That is a conclusion, rather than a
hypothesis,
if we use the gauge integral.
Actually, the hypotheses can be made even weaker: We can
allow
F to be nondifferentiable at countably many points. More
precisely: Assume F is continuous, and that G is some
function
defined at every point of [a,b], and that F'(t) exists
and
equals G(t) for all but at most countably many values
of t. Then the gauge integral
![[gif integral]](int.gif) ab G(t)dt
exists
and equals F(b)–F(a).
ab G(t)dt
exists
and equals F(b)–F(a).
![[gif improper integral]](improper.gif)
Thus, any "improper gauge integral" also exists as a proper one.
(Clarification: The function f must be defined at every point of [a,b]. In the case of f(t)=1/√t on the interval (0,1], we also assign some value to f(0). What value we assign doesn't really matter, just so long as f(0) is some particular number.)
But uniform convergence is a very strong assumption, so we usually teach our graduate students a result like this:
Suppose (fn) is a sequence of Riemann integrable functions on [a,b], converging uniformly to a limit f. Then f and |fn–f| are Riemann integrable, and as well.
We usually teach this to our graduate students under the additional assumption that the functions e and g are Lebesgue integrable; then the other functions are Lebesgue integrable too. However, the version of the theorem presented above can be stated (without proof) in undergraduate courses -- perhaps even in a freshman calculus course.
Dominated Convergence Theorem. Suppose (fn) is a sequence of gauge integrable functions, converging pointwise to a limit f. Also suppose that e(t) < fn(t) < g(t) for all n and t, where e and g are some gauge-integrable functions. Then f and |fn–f| are gauge integrable, and as well.
There are other convergence theorems for gauge integrals, involving hypotheses weaker than the domination condition e(t) < fn(t) < g(t), but those theorems are generally much more complicated. Research is still being done in that area.
Here are my opinions (substantially revised 11/16/00). The role of the gauge integral in our teaching must be viewed in terms of the way that we presently teach analysis. Here in the USA, we usually teach analysis on three levels:
![[gif
integral]](int.gif) ab F '(t)dt = F(b)–F(a);
any further clauses about continuity or differentiability
or existence of integrals are unnoticed by most students.
We show our calculus students that the characteristic
function of the rationals is not Riemann integrable
on (for instance) the interval [0,1], but
most of our calculus students have no idea what we are
talking about.
ab F '(t)dt = F(b)–F(a);
any further clauses about continuity or differentiability
or existence of integrals are unnoticed by most students.
We show our calculus students that the characteristic
function of the rationals is not Riemann integrable
on (for instance) the interval [0,1], but
most of our calculus students have no idea what we are
talking about.
Level (2), on the other hand, would be an excellent place to introduce the gauge integral. The conventional course at the advanced undergraduate level concentrates on the use of tools such as epsilons and deltas, convergent sequences, limsups and liminfs, etc. Those are the same tools used in the theory of the gauge integral. Thus, adding that integral to the course would only involve slight modifications in the course. The book by DePree and Swartz is particularly well suited for this purpose. Bartle and Sherbert, 3rd edition, is also applicable to this purpose, though it devotes slightly fewer pages to the gauge integral.
Introducing the gauge integral into level (3), the graduate course, might also be a good idea, but it would involve greater complication. The graduate course has its share of epsilons and limsups, but its most basic tools are topologies and sigma-algebras, a very different sort of thinking. The gauge integral does not generalize readily to abstract settings like abstract sigma-algebras. (It can be generalized to a setting something like that, but it then loses much of its wonderful simplicity.) In its simplest form, it is more like the Lebesgue integral with respect to Lebesgue measure, not other measures. Of course, Lebesgue measure is the most important measure. (Perhaps we should deemphasize the other measures in the first graduate course on integration theory, in order to make the gauge integral fit into the course more readily. Other measures can be developed in greater detail in a later course.)
I think that the two theories -- Lebesgue and gauge -- both are valuable, and both deserve to be covered in the graduate course. I'm not yet sure what is the best way to organize such a course. We can develop one of the two theories, and then use its results as tools in developing the other theory. This is the approach taken by Gordon's book (which develops the Lebesgue theory first) and by Bartle's "MTI" book and the Lee/Vyborny book (both of which develop the gauge theory first).
Of course, there are some obvious examples -- e.g., if we permit the function to be unbounded or if we permit its domain to be unbounded. But what about a bounded function on a bounded interval? Within this class of functions, it is hard to give an example of a function that is not integrable. It was already hard enough with the Riemann integral -- for that integral we had to use rather bizarre functions, such as the characteristic function of the rationals. Now, when we turn to the gauge integral or the Lebesgue integral, more functions are integrable, and so it is even harder to produce examples of non-integrable functions.
Actually, the problem is the same for gauge integrals or Lebesgue integrals. Indeed, when f is a bounded real-valued function on a bounded interval, then these three conditions are equivalent:
"every bounded function on a bounded interval is gauge integrable."Indeed, there do exist functions which contradict that conjecture, but it is extremely difficult to exhibit such a function.
Every introductory textbook on Lebesgue integrals includes a short proof (due to Vitali) of the existence of a nonmeasurable set; the characteristic function of that set is then a nonmeasurable function. But that proof, like every known proof of that theorem, is nonconstructive -- it uses the Axiom of Choice to prove the existence of the nonmeasurable function without actually "finding" the function or describing it explicitly. Vitali's proof is one of the most elementary uses of the Axiom of Choice, and perhaps it makes a good introduction to the Axiom of Choice; it could be included in an appendix in a book intended for some advanced undergraduate students. But I think this is conceptually way beyond the grasp of freshman calculus students. All we can do is tell these students: "Yes, there does exist a non-integrable, bounded function on a bounded interval, but describing it to you would require a great deal of higher math, far beyond the scope of this freshman calculus course."
You might notice that, in the last paragraph, I said that every known proof requires the Axiom of Choice. Is it possible that we may someday find another proof that is constructive? i.e., that we may find an explicit example of an unmeasurable function? Probably not. This is not just a personal opinion -- it has some supporting evidence, though the evidence is rather technical. Solovay proved in 1970 that the nonexistence of a nonmeasurable function is consistent with ZF set theory (i.e., conventional set theory minus the Axiom of Choice), provided that there exists an inaccessible cardinal. The existence of an inaccessible cardinal is empirically consistent with conventional set theory -- i.e., after many decades, no one has yet found a contradiction, so Solovay's model seems to be reliable. If you're interested, these topics are discussed a little more in my book, and more references are given there. -- My, we certainly seem to have gotten into some deep math, while discussing what to teach to freshmen!