(This web page was created using latex2html.
It contains
numerous inline gifs. To view it properly, use
a graphical browser such as Netscape or Explorer;
a text browser such as Lynx will not suffice.)
AN OPEN LETTER
To: The authors of calculus textbooks
From: Several authors of more advanced books and articles --
Robert Bartle, USA <mth bartle@emuvax.emich.edu>
Ralph Henstock, Ireland <r.henstock@ulst.ac.uk>
Jaroslav Kurzweil, Czech Republic <kurzweil@mbox.cesnet.cz>
Eric Schechter, USA <schectex@math.vanderbilt.edu>
Stefan Schwabik, Czech Republic <schwabik@beba.cesnet.cz>
Rudolf Výborný, Australia <R.Vyborny@mailbox.uq.edu.au>
Subject: Replacing the Riemann integral with the gauge integral
It is only an accident of history that the Riemann integral is
the one used in all calculus books today. The gauge integral
(also known as the generalized Riemann integral, the Henstock
integral, the Kurzweil integral, the Riemann complete integral,
etc.) was discovered later, but it is a "better" integral in
nearly all respects. Therefore, we would like to suggest that
in the next edition of your calculus textbook, you present both
the Riemann and gauge integrals, and then state theorems mainly
for the gauge integral.
This switch would only require altering a few pages in your
calculus book. Any freshman calculus book is devoted almost
entirely to derivatives and antiderivatives -- how to compute
them and how to use them; that material would not change at
all. The only changes would be in the more theoretical
sections of the book -- i.e., the definitions and theorems --
which take up only a few pages.
The reasons for making this change are twofold: (i) It would
actually make some parts of your book more readable. Some
definitions and theorems can be stated more simply (and more
strongly) if the gauge integral is used instead of the Riemann
integral. This is particularly true of the Second Fundamental
Theorem of Calculus, discussed below. (ii) It would be a better
preparation for the handful of calculus students who will go on
to higher math courses. The gauge integral is far more useful
than the Riemann integral, as a bridge to more advanced
analysis.
The idea of introducing the gauge integral to college freshmen
is not entirely new; it was promoted, for instance, in
the paper "The Teaching of the Integral" by Bullen and Výborný,
Journal of Mathematical Education in Science and Technology,
vol. 21 (1990). However, we feel that the idea deserves wider
promotion; hence this letter.
Introduction to the integral. If you are not already familiar
with the gauge integral, we would recommend the article by
Bartle in the American Mathematical Monthly, October 1996; it
provides a quick introduction to the subject and gives most of
the main references. Perhaps a second introduction would be the
book of DePree and Swartz (Introduction to Real Analysis, Wiley,
1988); it is written for advanced undergraduates and is probably
the most elementary among the currently available introductions
to this subject. Professors Bartle and Schechter have
volunteered to make themselves available, at least to some
extent, to answer further questions you may have about this
subject.
The definition. The gauge integral is a very slight
generalization of the Riemann integral. Instead of a constant
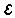 and a constant
and a constant 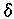 ,
it uses a constant
,
it uses a constant 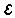 and a
function
and a
function 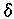 .
The two definitions can be formulated so that
they are nearly identical, and then placed side by side. This
would be helpful to the teachers who are using the book and
learning about the gauge integral for the first time.
.
The two definitions can be formulated so that
they are nearly identical, and then placed side by side. This
would be helpful to the teachers who are using the book and
learning about the gauge integral for the first time.
We think that the slight increase in the complexity of
the definition will make little difference to the students
learning from the book. It has been our experience that, for
the most part, freshman calculus students do not fully grasp the
definition of the Riemann integral anyway; it is just too
complicated for students at that level. The definition of the
Riemann integral is included in a calculus book more for
completeness and integrity than for teaching. The few students
who have enough mathematical maturity to grasp the definition of
the Riemann integral will probably have no greater difficulty
with the gauge integral, and they will benefit from being
exposed to this concept in their calculus book.
Existence and nonexistence of integrals. In recent calculus
books it is customary to state without proof that continuous
functions and monotone functions on a compact interval are
Riemann integrable. The omission of the proofs is unavoidable
-- a proof would involve the completeness of the reals, uniform
continuity on compact intervals, and other notions that are far
beyond the reach of freshmen.
Any Riemann integrable function is also gauge integrable. Many
more functions are gauge integrable, as will be evident later in
this letter; see especially our remarks about the Dominated
Convergence Theorem.
It is customary to give the characteristic function of the
rationals as an example of a function that is not Riemann
integrable. Most students don't fully understand this example,
because the characteristic function of the rationals is too
unlike familiar examples to appeal to the intuition of most
students. Still, it is useful to include such an example in the
book, because the student comes away convinced (perhaps through
trust rather than through understanding) that
not every bounded function
on a closed bounded interval is Riemann integrable.
A book covering the gauge integral might still include the
characteristic function of the rationals, as an example of a
bounded function that is gauge integrable but not Riemann
integrable on a closed bounded interval.
Ideally, one would like to also include a concrete example of a
bounded function that is not gauge integrable on a closed
bounded interval. Even if it is complicated, the presence of
such an example would convince the student (again, through
trust) that not every function is gauge integrable.
Unfortunately, there are no concrete examples, as explained
later in this letter. That is both a strength of the theory
(essentially all functions are gauge integrable) and a weakness
of the theory (it is hard to convey the concept of the few
functions that are not gauge integrable).
The book might include a statement something like this:
"Heuristically, every bounded function that one is likely to
encounter in applications is gauge integrable on any closed
bounded interval. Although it is possible to prove
mathematically that there exist bounded functions that are NOT
gauge integrable on closed bounded intervals, such functions do
not arise in practical applications. We shall discuss this
further, briefly, in the appendix." Some possibilities for the
appendix are discussed later in this letter.
The first fundamental theorem of calculus: derivatives of
integrals. There are two versions of this
theorem -- an elementary version and a
more advanced version. The elementary version is this:
Suppose 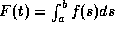 exists. Then F is continuous.
Moreover, at every t
where f(t) is continuous, the derivative F '(t) exists
and equals f(t).
exists. Then F is continuous.
Moreover, at every t
where f(t) is continuous, the derivative F '(t) exists
and equals f(t).
We don't have to assume f is continuous everywhere. The theorem is
not hard to prove. A remark might be made that "a more advanced and
stronger version of this theorem can be found in the appendix."
The more advanced version says:
Suppose 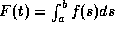 exists. Then F is continuous.
Moreover, at almost every t,
the derivative F '(t) exists and equals f(t).
exists. Then F is continuous.
Moreover, at almost every t,
the derivative F '(t) exists and equals f(t).
("Almost every" would have to be defined in the appendix.)
We don't have to make any assumption at all about continuity of
the integrand, f.
However, this more advanced version is harder to prove;
you'd have to just state it without proof.
The second fundamental theorem of calculus: integrals of
derivatives. Here the gauge integral offers a big advantage
over the Riemann integral. Again there are two versions.
The elementary version is:
If f(t)=F '(t)
exists for all t in [a,b], then
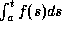 exists and equals F(t)-F(a).
exists and equals F(t)-F(a).
We don't have to make any assumption of continuity of f.
The proof of this theorem is easy
enough to include in a freshman calculus book.
In an appendix, after introducing countable sets, you
could state and prove this advanced version:
Suppose F is continuous. Also suppose
f(t)=F '(t) exists for all but countably
many points t in [a,b]; define f
arbitrarily at those points. Then
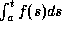 exists and equals F(t)-F(a).
exists and equals F(t)-F(a).
The proof is not very hard. (By the way, in this theorem, "for
all but countably many points" cannot be replaced by
"except on a set of measure 0"; that is shown by the Cantor
Function.)
Convergence theorems. Calculus books traditionally have
included the theorem that uniform limits preserve integrability
and integrals. However, for the gauge integral we can state
this much nicer and stronger Dominated Convergence Theorem:
Suppose 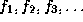 are gauge
integrable functions on [a,b], converging
pointwise to a limit function f. Suppose
that
are gauge
integrable functions on [a,b], converging
pointwise to a limit function f. Suppose
that 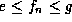 for all n, where
e and g are gauge integrable functions.
Then f is gauge integrable, and
for all n, where
e and g are gauge integrable functions.
Then f is gauge integrable, and
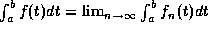 .
.
Thus, under rather simple and mild assumptions, pointwise limits
preserve integrability and integrals. This theorem can be used
to demonstrate the integrability of a very wide class of
functions.
The Monotone Convergence Theorem and Dominated Convergence
Theorem could be stated without proof, and then examples and
exercises can be given. Applications can be found in any book
on the Lebesgue integral.
(Actually, the Monotone and Dominated Convergence Theorems are
also true, in appropriate forms, for Riemann integrals. Some
references can be found in a paper by Simons, Math.
Intelligencer 17 (1995), 67-70. However, the proofs in that
setting are not much shorter than the proofs in the more general
setting of gauge or Lebesgue integrals, and so there is not
much reason to bother with them in an introductory course.)
Improper integrals. A separate definition is not required. A
statement such as
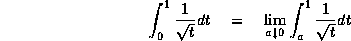
becomes a
theorem, rather than a definition of the left side of the
equation. Admittedly, we still end up using the right side of
the equation as a method for computing numerical values, but it
is conceptually advantageous to have this equation as a theorem
instead of a definition.
A separate definition can also be avoided for integrals over
unbounded intervals. A statement such as
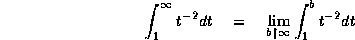
becomes a theorem, rather than a definition of the left side of
the equation, if the definition of the integral is formulated as
in McLeod's book -- i.e., unbounded subintervals make 0
contribution to the approximating Riemann sum. (Admittedly,
this may be counterintuitive to beginners, so it is perhaps
debatable whether this more general definition is desirable in a
calculus textbook.)
Integration formulas. Any calculus book must include the
substitution rule (i.e., change of variables or
reparametrization in integrals) and integration by parts.
Usually these are stated as computational formulas, with the
regularity hypotheses glossed over. If one does wish to state
the regularity hypotheses explicitly, those hypotheses can be
weakened slightly by switching from Riemann integrals to gauge
integrals.
Appendices. At the end of your book you may wish to add a few
pages of material which has not customarily appeared in calculus
books. This is more for the benefit of the teachers and
occasional gifted students than for the typical student. Here
is an outline of some suggested material:
Countability. It would be helpful to discuss the difference
between countable and uncountable sets. Examples would include
the fact that the integers and the even integers are
equipollent; Cantor's proofs that the rationals are countable
but the reals are not. The union of countably many countable
sets is countable. The gauge integral of the characteristic
function of any countable set is 0. These results are not hard
to prove.
Anticipating results below about measure, you might also prove
that the Cantor set is uncountable. (To simplify the
exposition, remove the middle 8/10 instead of the middle 1/3;
then you can use decimal expansions instead of ternary
expansions.)
A theorem of Cantor states that any set has smaller cardinality
than its power set. The proof is is actually very short and
easy, except that it is rather abstract.
Measure. A set is measurable if and only if its characteristic
function is gauge integrable; then the measure of the set is
equal to the value of that integral. Easy examples show that
this extends the notion of length, and gives us a notion of "size"
for a very large class of subsets of the real line.
Admittedly, defining size in terms of integrals is conceptually
backward -- many mathematicians find it more intuitive to
define integrals in terms of measures -- but for purposes of
your calculus book, this approach saves several pages.
Some basic properties can be stated, with or without proof. The
union of countably many disjoint measurable sets is measurable,
and its measure is the sum of their measures; etc. If a
function vanishes outside a set of measure 0, then that function
is gauge integrable and its integral is 0. Any countable set has
measure 0. The Cantor set is an uncountable set with measure 0,
since it is contained in simpler sets with arbitrarily small
positive measure.
Unmeasurable sets. Vitali's classical proof of the existence of
an unmeasurable set is fairly short and elementary. It can be
found in any book on Lebesgue integration. A sketch of the
proof might be useful in the appendix to a calculus book. The
typical calculus student would not understand the proof, but a
few students might understand a few parts of the proof. In any
case, the student would go away believing (perhaps on
trust rather than on understanding) that there do exist
unmeasurable sets.
Vitali's proof uses the Axiom of Choice in a fairly simple and
intuitive way. The expositor can point out the Axiom
of Choice when it is used, and emphasize that the proof is not
constructive. It can be stated that there are no
constructive ways of obtaining unmeasurable sets.
(The proof of the fact that there are no
constructive ways is rather difficult; it involves much
set theory and logic. It is discussed in part of
Schechter's book, Handbook of Analysis and its Foundations,
Academic Press, 1996.)
Thus, we know that there exist bounded functions that are
not gauge integrable on a closed bounded interval, but we cannot
produce explicit examples of such functions.
In summary, we feel that the changes in the calculus book would
not be major but would improve the teaching of calculus. We
invite your questions on these matters.
Sincerely,
Robert Bartle, Ralph Henstock, Jaroslav Kurzweil, Eric Schechter,
Stefan Schwabik, and Rudolf Výborný
(This letter is being distributed to publishers' representatives
at the Joint Mathematics Meetings in San Diego, California, in
January 1997. We may also try to publish it and/or distribute
it in some other fashion in the near future, perhaps with slight
modifications and/or more signatures.)
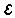 and a constant
and a constant 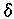 ,
it uses a constant
,
it uses a constant 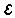 and a
function
and a
function 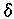 .
The two definitions can be formulated so that
they are nearly identical, and then placed side by side. This
would be helpful to the teachers who are using the book and
learning about the gauge integral for the first time.
.
The two definitions can be formulated so that
they are nearly identical, and then placed side by side. This
would be helpful to the teachers who are using the book and
learning about the gauge integral for the first time.