I am not a leading researcher on infinite sets, but I nevertheless attract a fair amount of email on the subject; I imagine this is mostly because I have posted several web pages on related subjects. Much of the email consists of arguments against the notion of a completed infinity. On this web page I will try to clarify that subject, so that I don't have to spend so much time answering email. (The first version of this web page was written on May 7, 2005; the page probably will evolve over the next few months as I respond to comments.)

• Potential infinity refers to a procedure that gets closer and closer to, but never quite reaches, an infinite end. For instance, the sequence of numbers

  1, 2, 3, 4, ...

  gets higher and higher, but it has no end; it never gets to infinity. Infinity is just an indication of a direction -- it's "somewhere off in the distance." Chasing this kind of infinity is like chasing a rainbow or trying to sail to the edge of the world -- you may think you see it in the distance, but when you get to where you thought it was, you see it is still further away. Geometrically, imagine an infinitely long straight line; then "infinity" is off at the "end" of the line. Analogous procedures are given by limits In calculus, whether they use infinity or not. For example, lim_{x to 0} (sin x)/x = 1. This means that when we choose values of x that are closer and closer to zero, but never quite equal to zero, then (sin x)/x gets closer and closer to one.

• Completed infinity, or actual infinity, is an infinity that one actually reaches; the process is already done. For instance, let's put braces around that sequence mentioned earlier:

  { 1, 2, 3, 4, ... }

  With this notation, we are indicating the set of all positive integers. This is just one object, a set. But that set has infinitely many members. By that I don't mean that it has a large finite number of members and it keeps getting more members. Rather, I mean that it already has infinitely many members.

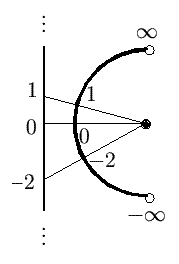
  We can also indicate the completed infinity geometrically. For instance, the diagram at right shows a one-to-one correspondence between points on an infinitely long line and points on a semicircle. There are no points for plus or minus infinity on the line, but it is natural to attach those "numbers" to the endpoints of the semicircle.

  Isn't that "cheating," to simply add numbers in this fashion? Not really; it just depends on what we want to use those numbers for. For instance, f(x)=1/(1+x²) is a continuous function defined for all real numbers x, and it also tends to a limit of 0 when x "goes to" plus or minus infinity (in the sense of potential infinity, described earlier). Consequently, if we add those two "numbers" to the real line, to get the so-called "extended real line," and we equip that set with the same topology as that of the closed semicircle (i.e., the semicircle including the endpoints), then the function f is continuous everywhere on the extended real line. This has some advantages in advanced mathematics: The topology of the closed semicircle is compact and metrizable. Compact metric spaces have very nice topological properties; for instance, every sequence has a convergent subsequence. Even if we're really just interested in the properties of the ordinary (finite) real numbers, we can discover and prove some of those properties more easily by viewing that set of numbers as a subset of this larger, compact metric space.

History and controversy

Infinity cannot be experienced in our everyday lives, but infinity might be a good "approximation" to some of the quantities that we read about in the news. There are 7 billion people in the world, and the annual national budget is several trillion dollars, and the national debt is many trillions of dollars; all of these numbers are much bigger than most of us -- even mathematicians -- have any real feeling about. And the number of atoms in the earth is much much bigger than trillions; I don't even know the name for that number. But still these numbers are finite.

Nor can we experience the infinitely small in our lives. In fact, the currently prevailing theories of quantum physics tell us that there is a lower limit, a smallest physical object.

If we don't see infinity in the physical world around us, then where do we see it? Why, in our heads, of course. Actually, we see all of mathematics in our heads. We may see three airplanes or three apples in the physical world, but the abstract notion of "3" does not exist in the physical world -- it only exists in our minds. The notion of "3" is simple enough, and is an abstraction of enough concrete objects, that there is little chance of our disagreeing on the notion. Our conversations seem to suggest that the "3" in my head is very much like the "3" in your head (though we will never be 100% certain of that). But more complicated notions such as infinity, less grounded in physical reality, are harder to explain; it is harder to be sure that we are successfully conveying a concept from the inside of one head to the inside of another.

Cantor's discoveries about infinite sets were just part of a deeper philosophical revolution that affected all branches of mathematics, not just set theory. New conventions became fashionable, governing what kinds of imaginary worlds mathematicians would permit inside their heads. In effect, formalism replaced Platonism. Many mathematicians today still believe themselves to be Platonists, and perhaps they can afford that luxury if they work in a small enough portion of mathematics; but the predominant paradigm of mathematics as a whole has shifted toward formalism. The birth of mathematical formalism is most often associated with David Hilbert (1862-1943), but I think much credit for it is owed to Cantor, and also to a less well known geometer, Eugenio Beltrami (1835-1900).

• Probably I am using the word "Platonism" slightly differently from the way that it is used by philosophers. By mathematical Platonism I mean the view that mathematics is an attempt to describe some sort of reality, some sort of absolute truth --- and that there is, in fact, just one correct absolute truth. Perhaps a better word would be monism, emphasizing that there is only one truth. This was the predominant view until the late 19th century. For instance, geometry was our best attempt at describing physical space, and it was certainly Euclidean. Any non-Euclidean geometry was obviously wrong, a pack of lies, at best a work of fiction. In fact, before Beltrami's time, considerable effort was spent in trying (unsuccessfully) to show that the axioms of any non-Euclidean geometry must inevitably yield a contradiction.

• By formalism I mean the view that mathematics does not need to be grounded in physical reality. We can start from whatever axioms we like (though we are urged to at least exercise some good taste in choosing our axioms). We then investigate what consequences can be proved from our axioms. Perhaps a better term for this viewpoint would be pluralism, referring to the fact that there can be many truths. For instance, the sum of the three angles of a triangle add up to exactly two right angles if you're working on a Euclidean plane, or more than two right angles if you're working on the surface of a sphere, or less than two right angles if you're working on a saddle surface. (In the last two cases, you don't have straight lines, so you have to redefine "triangle." For the side of a triangle, use the shortest path between two vertices of the triangle.) Beltrami's 1868 paper showed that certain non-Euclidean systems of axioms are modeled (i.e., satisfied) within Euclidean geometry by spheres, saddles, etc. From this mathematicians saw that the non-Euclidean axioms cannot lead to a contradiction (unless Euclidean geometry itself is contradictory).

Formalism and its consequences were controversial at first. One of the more visible battle lines was between the group now known as classicists (who believe that mathematics is a collection of statements) and constructivists (who believe that mathematics is a collection of constructions or procedures). The overwhelming majority of mathematicians today are classicists, but this is merely a matter of personal preference (like one's favorite color), not a matter of someone being right or wrong. Nearly any mathematician today who understands both sides of the issue agrees that both sides make perfectly good sense. (On the other hand, many classicists today are entirely unfamiliar with the constructivist viewpoint.)

A striking example is the Axiom of Choice (described in greater detail on another web page). This axiom, acceptable to classicists but not to constructivists, is a nonconstructive assertion of the "existence" of certain sets or functions. The use of the word "exist" is merely a grammatical convenience here; mathematicians and nonmathematicians do not mean quite the same thing by this word. Unfortunately, we mathematicians don't have a better word; to be more precise we would have to replace this one word with entire paragraphs. If we assume the Axiom of Choice, we are not really stating that we believe in the physical "existence" of those sets or functions. Rather, we are stating that (at least for the moment) we will agree to the convention that we are permitted write proofs in a style as though those sets or functions exist.

Whether those sets or functions "really" exist is actually not important, so long as they do not give rise to contradictions. Mathematicians are perfectly willing to use devices that may be fictional, as intermediate steps in getting from a real problem to a real solution. Perhaps the most striking example of this is the use of so-called "imaginary numbers" such as i, the square root of -1 (described in greater detail on another web page). Such numbers were first developed for the purpose of solving certain polynomial equations. Initially, the attitude mathematicians took was, "there cannot really be a square root of -1, but if such a number did exist, what would its properties be?" Many decades later, it was discovered that those properties correspond, in a natural way, to the process of rotating the Euclidean plane through a quarter turn. The number i is very useful to engineers, for solving differential equations involving sines, cosines, and other functions related to rotation. That's very real, not at all fictitious. Nevertheless, the name "imaginary" stuck.

The formalist revolution took longer to reach some branches of mathematics than others. One of the late arrivals was mathematical logic. One type of logic, now known as "classical logic," was given almost exclusive sovereignty until perhaps as late as 1960, and only gradually began to share its power with nonclassical logics during the last decades of the 20th century. Perhaps this delay was caused by the fact that, around 1930, Kurt Gödel made some highly interesting and important contributions to classical logic, thereby distracting people away from other logics. Classical logic is adequate for the needs of most mathematicians, and it is computationally the simplest of the main logics, but it disregards qualities such as constructiveness, relevance, and causality. The study of those qualities has led to alternative logics, some of which are discussed further on the web page advertising my logic book.

Though the formalist revolution is an undeniable fact of mathematical (and perhaps scientific) history, some questions about it still remain -- e.g., is formalism good or bad? Some scientists and mathematicians have suggested that mathematics, no longer tied to its origins in physics, is developing into a baroque art form, a thing of great embellishments and few uses; that mathematics has been reduced to a mere game of meaningless marks on paper. Others have argued that mathematics turns out to be useful in surprising and unexpected ways, just because mathematicians have concerned themselves with the investigation of the fundamental properties of basic mathematical objects, such as numbers. Perhaps the most famous essay on this subject is The Unreasonable Effectiveness of Mathematics in the Natural Sciences, published in 1960 by Eugene Wigner.