
0-691-12279-2
(ISBN-10) |
Prospective reviewers and teachers should contact Vickie_kearn@pupress.princeton.edu for copies.
This is an introduction to mathematical logic, intended for undergraduate students with no previous knowledge of logic. This treatment replaces the traditional depth-first approach with a breadth-first (but not shallow!) approach which I believe is more intuitive and understandable for the students.
Free excerpt (471 kb PDF): Chapter 1, the introduction for teachers, discusses further how this book differs from other logic books. Chapter 2, the introduction for students, might be useful by itself as a brief introduction to logic (regardless of whether you buy the book).
Also downloadable: The most recent version of a 1-hour introductory talk that I have presented to some undergraduate math clubs. For TeX enthusiasts, here's the source file.
Should we use this book for our "how to do proofs" course? No, I recommend against using any logic book for that purpose. I'd explain that with this analogy: A book on organic chemistry will tell you "what is really going on" in your kitchen, but a conventional cookbook is more useful if you want to learn to prepare food. Likewise, a course in logic will explain "why proofs work the way they do" -- but for the skills of doing ordinary mathematical proofs, I'd recommend some ordinary math (e.g., general topology), taught using the Moore method.
CAUTION: This book does not fit the traditional syllabus for an introductory logic course. It should only be adopted by teachers who are aware of the differences and are persuaded of this book's advantages.
Before the 20th century, mathematicians saw their work mostly as empirical or descriptive, an uncovering of the laws of the physical universe; each question had only one correct answer. Logic was seen as an explanation of reasoning, and few people could see room for more than one explanation. So-called "classical" logic, developed by Frege, Russell, and others, was the dominant paradigm of logic. Well into the late 20th century, the "one logic only" viewpoint persisted, though a few isolated mathematicians -- Brouwer, Lukasiewicz, Belnap, etc. -- pursued different, nonclassical visions of what "the one true logic" should be.
The formalist revolution began with non-Euclidean geometries in the late 19th century and spread gradually through mathematics. Mathematicians began to see that the physical universe is neither knowable nor necessary to their work. Mathematics came to be viewed as a game of marks on paper, or an investigation of pure thought; different assumptions yield different theories. By the late 20th century, this change of philosophy had spread to logic. Researchers saw different logics merely as different types of abstract structures, no longer requiring philosophical justifications. Gradually, without fanfare, the pluralist (many logics) viewpoint became prevalent in research literature.
It is understandable that
textbooks change slowly and lag behind research.
Most new research
discoveries are too specialized and advanced to be
appropriate for beginners. Thus, most of today's
introductory logic textbooks still concentrate on just
classical logic, focusing mainly on ideas of Gödel
(1930's) and earlier. Nonclassical logics can be found only
in more advanced books and in research journals, heavily
algebraic and inaccessible to beginners.
But I believe the pluralist
approach to logic is important enough, and can be
reformulated to be elementary enough, for beginners;
that is the goal of my book.
I am attempting to bring to the beginners' classroom a
revolution which occurred in the research literature
during the last few decades.

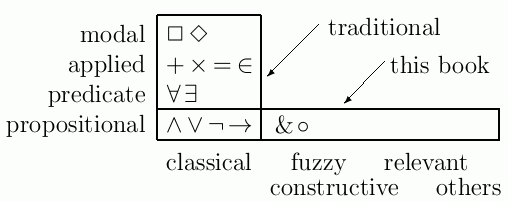
A first course in logic should aim at teaching, not just some particular logic or logics, but some deeper ideas that apply to all logics --- interpretation, derivation, completeness, etc. The traditional and pluralist approaches share those deeper goals. But on a more superficial level, the traditional and pluralist approaches have rather little overlap --- see the diagram at right. The pluralist approach gains breadth by sacrificing some depth. Of course, a logician needs both breadth and depth, but both cannot be acquired in the first semester. I am convinced that the breadth-first approach is better for most students, not only for obvious philosophical reasons, but also for pedagogical reasons outlined below.
Thought is so complicated that we may never understand it completely, but some of its ingredients are simple enough to identify and analyze. Ordinary human thought (including that of mathematicians!) is not just classical logic, but a mixture of many logics. Here are some examples:
| ||||||||||||||||||||||
When classical logic is presented by itself, it not only seems artificial, but also takes on the aura of "absolute truth," leaving no room for doubt. But reasoning requires doubt; ideally we should teach our students to question everything. In mathematics one must constantly ask:
What if this condition is not true? What happens then?
But that question is rather abstract and hypothetical. It is difficult for beginning students. Even for advanced students or experienced researchers, such a question by itself is seldom productive. It must be supported by the more concrete question,
What happens differently in the other examples that we have studied?
It is a basic pedagogical principle — not just in logic, but in any subject — that any abstract idea is best taught with several different examples; one example (classical logic) is hardly enough. Contrasts between different logics make some properties easier to understand. For instance, the properties listed in the table below are explained and proved in CNL; the explanation is made clearer by the fact that the properties take different forms in different logics.
| properties →
logics ↓ |
Excluded Middle: |
Deduction Principle: If |
If A, B share no variables, and |
Explosion: |
| relevant | yes | can't happen | no such result | |
| RM | yes | |||
| constructive | No. But if then |
|||
| Wajsberg | no consequence | |||
| classical | yes | all of the above |
A traditional course on logic may end by covering Gödel's Incompleteness Theorems. But I believe that most of the students in such a course -- though perhaps able to follow the individual steps -- have difficulty understanding the overall concept of incompleteness, chiefly because it is preceded by too few examples of completeness. CNL presents many examples of completeness. By "completeness" I mean a pairing of some semantic system with some syntactic system, such that
| Syntactics (axioms) | Semantics (interpretation) | Completeness? |
| classical | 2-valued; powerset-valued; hexagon | proved in book |
| constructive | all topologies; all finite topologies; one infinite topology | proved in book |
| relevant | crystal matrix | soundness proved; also proved that no finite matrix is adequate |
| RM | Sugihara's Z-valued | completeness stated; soundness proved |
| Rose-Rosser axioms | Lukasiewicz [0,1]-valued | completeness stated; soundness proved |
| Wajsberg axioms | Lukasiewicz 3-valued | completeness proved in book |
| relevant implication; constructive implication | worlds models | completeness proved in book |
| no findable axiomatization | arithmetic | Gödel's 1st Incompleteness, stated |
As we remarked earlier, the semantics of propositional logic is very simple, and gets only a few pages in a traditional, classical-only book. When we turn to nonclassical logics, semantics becomes a much richer and more interesting subject, but it remains fairly concrete and accessible to beginners. Consequently semantics can be used as motivation for the more abstract subject of syntactics. CNL studies semantics for several chapters before even starting syntactic logic.
CNL begins with
prerequisite material -- informal set theory and a few
basics of topology -- so that it is self-contained,
and suitable for a nonhomogeneous class or for
self-guided study.
The book is intended for
beginners, so it keeps algebra to a minimum.
For instance, it uses topologies instead of
Heyting algebras, because they are more
concrete and easier to define.
The logics that are developed in the book
were selected not for their appealing
algebraic structures, but for their
philosophical and psychological motivation,
their connections to the premathematical experience
of students, who may have very little
previous mathematical training. That premathematical
experience cannot be used as an ingredient
in proofs, but it can be used to supply intuition,
which is crucial for beginners.
Still, after the motivating introductory
chapters, CNL is a book
of mathematics; all results are rigorously
proved.