In order to analyze an arbitrary diagram over H=Hm,n, and
![]() in general we change the presentation of
H. We add all words K(u) (discs) and all relations of
in general we change the presentation of
H. We add all words K(u) (discs) and all relations of
![]() to the presentation.
The presentation becomes infinite. After that we order the relations, saying
that the discs have the highest rank, r-relations have smaller ranks, and the b-commutativity relations have the lowest rank. With every diagram we associate its type, a vector, the first coordinate of which is the number of discs, and the last coordinate
is the number of b-commutativity cells (we omit the ranking of other relations). It turns out that diagrams of minimal type have nice geometric properties.
to the presentation.
The presentation becomes infinite. After that we order the relations, saying
that the discs have the highest rank, r-relations have smaller ranks, and the b-commutativity relations have the lowest rank. With every diagram we associate its type, a vector, the first coordinate of which is the number of discs, and the last coordinate
is the number of b-commutativity cells (we omit the ranking of other relations). It turns out that diagrams of minimal type have nice geometric properties.
The main and easy concept which helps us analyze these diagrams is the
concept of a band 3.
If S is a set of letters then an S-band is a
sequence of cells
![]() in a van Kampen diagram such that each
two consecutive cells in this sequence have a common edge labeled by a
letter from S. Figure 7 illustrates this concept.
in a van Kampen diagram such that each
two consecutive cells in this sequence have a common edge labeled by a
letter from S. Figure 7 illustrates this concept.
![]()
The broken line formed of the intervals
![]() ,
,
![]() is called the median of this
band.
is called the median of this
band.
We say that two bands cross if their medians cross. We say that a band is an annulus if its median is a closed curve. In this case the first and the last cells of the band coincide (see Figure 8)
Let S and T be two disjoint sets of letters, let (![]() ,
,
![]() ,
...,
,
...,
![]() ,
,
![]() )
be an S-band and let (
)
be an S-band and let (![]() ,
,
![]() ,
...,
,
..., ![]() ,
,
![]() )
is a T-band. Suppose that:
)
is a T-band. Suppose that:
For example, the diagram on Figure 9 contains k-bands, qi-bands, A-bands crossing the circles transversally, and r-annuli filling the space between consecutive circles. In the diagram on Figure 9 we also have a ![]() -annulus going around the disc, and many b-bands consisting of the b-commutativity cells.
-annulus going around the disc, and many b-bands consisting of the b-commutativity cells.
The main idea is the following. In most relations of the presentation of H one can choose two pairs of letters which belong to disjoint sets of letters. For example, the relation aba-1b-1=1 has a pair of a-letters and a pair of B-letters. The cells corresponding to these relations must form a-bands and b-bands in a van Kampen diagram. Each cell is an intersection of an a-band and a b-band. Thus if we prove that the number of a-bands is ``small" and the number of b-bands is ``small", and that an a-band and a b-band can have at most one common cell, we show that the number of (a,b)-commutativity cells is ``small".
In order to bound the number of bands we use the following idea. Suppose that we have ruled out annuli. Then every band starts (ends) either on the boundary of the diagram (the number of such bands is linear in terms on the perimeter), or on the boundary of a cells (for example, an a-band can end on a disc). This gives us the direction in which to proceed.
First we assume that a diagram contains no discs and prove the absence of certain types of annuli: r-annuli, ![]() -annuli, a-annuli, (r,a)-annuli, etc. (22 different kinds altogether). One way to prove it is to use a simultaneous induction: assume that one of these
annuli exists, take the innermost annulus of one of these kinds. Then the subdiagram bounded
by this annulus does not contain annuli of any of the 22 kinds. This makes the subdiagram look
nice and eventually leads to existence of a pair of cells that cancel (thus the diagram is not reduced which contradicts its minimality).
-annuli, a-annuli, (r,a)-annuli, etc. (22 different kinds altogether). One way to prove it is to use a simultaneous induction: assume that one of these
annuli exists, take the innermost annulus of one of these kinds. Then the subdiagram bounded
by this annulus does not contain annuli of any of the 22 kinds. This makes the subdiagram look
nice and eventually leads to existence of a pair of cells that cancel (thus the diagram is not reduced which contradicts its minimality).
Then we assume that the diagram contains discs and we bound the number of discs (see below) and their perimeters. Then we bound the number of r-bands by proving that there are no r-annuli, so each of the r-bands must start and end on the boundary of the diagram. Similarly we bound the number of ![]() -bands. Then we bound the
number of q-bands (they can start on the discs, and the perimeters of the discs are already bounded). Since every q-cell is an intersection of an r-band or a
-bands. Then we bound the
number of q-bands (they can start on the discs, and the perimeters of the discs are already bounded). Since every q-cell is an intersection of an r-band or a ![]() -band and a q-band, we bound the number of q-cells. This leads to a bound of the number of A-bands (they can end on q-cells and on discs), and so on.
-band and a q-band, we bound the number of q-cells. This leads to a bound of the number of A-bands (they can end on q-cells and on discs), and so on.
Of course we always need the absence of multiple intersections of bands. Although the next Figure 9 shows that a multiple intersection of an S-band and a T-band does not necessarily produce an (S,T)-annulus, it turns out to be enough to rule out (S,T)-annuli.
in
In order to bound the number of discs (and their perimeters) in a van Kampen diagram, we use the following idea.
The generic diagram over the presentation of H looks like this:
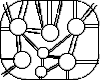
Discs in the diagram are connected by k-bands.
So with every van Kampen diagram we can associate a graph of discs. The vertices of this graph are the discs plus one external vertex. Vertices are connected by the k-bands. If a k-band starts on a disc and ends on the boundary of the diagram, we assume that this band terminates in the external vertex. The degree of each internal vertex of this graph is N>>1. We prove that this graph cannot have bigons: two discs connected by a pair of k-bands. This implies that the graph of discs is hyperbolic, and a standard small cancellation theory applies [25]. In particular there exists a disc with N-3 external edges. This also implies that the number of discs and k-bands in the diagram is linear in terms of the perimeter.
In order to rule out r-annuli, ![]() -annuli and other types of annuli,
we use several type reducing surgeries on a diagram.
One of them is illustrated by the following picture.
-annuli and other types of annuli,
we use several type reducing surgeries on a diagram.
One of them is illustrated by the following picture.
Moving r-bands. Suppose that in a minimal diagram ![]() an r-band
an r-band ![]() touches a disc
touches a disc ![]() as in
Figure 11 (that is one of the sides of
as in
Figure 11 (that is one of the sides of ![]() has two common k-edges with the contour of the disc).
Then it can be proved that
the bottom path of
has two common k-edges with the contour of the disc).
Then it can be proved that
the bottom path of ![]() has a common subpath with the contour of
has a common subpath with the contour of ![]() starting and ending with k-edges. Let p be the maximal common
subpath with this property, so that
starting and ending with k-edges. Let p be the maximal common
subpath with this property, so that
![]() ,
,
![]() .
Without loss of generality we can assume that the label
.
Without loss of generality we can assume that the label
![]() of
the path p has the form
kiwki+1w'ki+2...kjwhere
w=uq1uq2uq3Then for some word V we have that
of
the path p has the form
kiwki+1w'ki+2...kjwhere
w=uq1uq2uq3Then for some word V we have that
![]() is a cyclic shift of
is a cyclic shift of
![]() .
One can construct
an r-band
.
One can construct
an r-band
![]() with the bottom path labeled by the word Vand the r-edges having the same labels as in
with the bottom path labeled by the word Vand the r-edges having the same labels as in ![]() .
Let
.
Let
![]() be
the subband of
be
the subband of ![]() with bottom path p, so
with bottom path p, so
![]() .
Let ebe the start edge of
.
Let ebe the start edge of
![]() and let e' be the end edge of
and let e' be the end edge of
![]() .
Cut
the diagram
.
Cut
the diagram ![]() along the path
e-1p1 e'. We can fill the resulting
hole by gluing in the r-band
along the path
e-1p1 e'. We can fill the resulting
hole by gluing in the r-band
![]() and the mirror image
and the mirror image
![]() of
of
![]() .
The new diagram
.
The new diagram ![]() that we obtain this way
will have two r-bands instead of the old r-band
that we obtain this way
will have two r-bands instead of the old r-band ![]() .
The
first is
.
The
first is
![]() (the inverse band
(the inverse band
![]() differs from
differs from
![]() by the order of cells)
and the second one is
by the order of cells)
and the second one is
![]() .
The second r-band is an annulus
which touches
.
The second r-band is an annulus
which touches ![]() along its inner boundary. If we replace the disc
along its inner boundary. If we replace the disc ![]() by the corresponding van Kampen diagram over the presentation of
by the corresponding van Kampen diagram over the presentation of
![]() ,
we
see that the subdiagram
,
we
see that the subdiagram ![]() bounded by the outer boundary of the annulus
bounded by the outer boundary of the annulus
![]() is a diagram over the presentation of
is a diagram over the presentation of
![]() with exactly
one hub and no r-edges on the boundary. Then one can prove that
with exactly
one hub and no r-edges on the boundary. Then one can prove that
![]() is a disc (corresponding to some computation).
We replace it by one cell of the infinite presentation of H.
Then we reduce the resulting diagram.
is a disc (corresponding to some computation).
We replace it by one cell of the infinite presentation of H.
Then we reduce the resulting diagram.
![\begin{picture}(84.50,56.00)
\put(7.33,33.08){\oval(9.33,15.83)[l]}
\put(20.16,3...
...7.67,42.16){\line(-1,2){1.20}}
\put(77.50,52.66){\line(0,1){2.20}}
\end{picture}](img234.gif)
This construction amounts
to changing the disc ![]() ,
moving the band
,
moving the band ![]() through the disc and then reducing the resulting diagram.
through the disc and then reducing the resulting diagram.
Now suppose that there exists an r-annulus in our van Kampen diagram as in Figure 12.
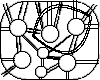
Suppose that there are discs inside the region bounded by this annulus. Then these discs form a hyperbolic graph, and so the r-band will intersect more than 1/2 of the k-bands going out of one of these discs. Then the r-band moving construction reduces the type of the diagram. Thus the region bounded by the r-annulus cannot contain discs. But we have ruled out the case when a diagram without discs contains an r-annulus, a contradiction.
In order to bound the perimeters of discs and B-cells we use the following
idea. The contour of a disc contains a constant number of non A-edges. Thus in order to
bound the perimeter of a disc, we need to bound the number of A-edges on the contour of it.
Every A-edge on the contour of a discs is the start edge of an a-band. An a-band consists
of a-commutativity cells corresponding to relations of the form ab=ba, ar=ra or
![]() or to the relations of the form
or to the relations of the form ![]() .
Thus an a-band can end either on a disc or on the boundary of a (a,q,r)-cell. The latter belongs to an r-band and we already know that the diagram contains only a ``small number" of r-bands. Thus if the a disc has a very big perimeter and many of the a-bands starting on the contour of this disc end on boundaries of (a,q,r)-cells, then many of these a-bands must end on the contour of the same r-band. The following lemma shows that it is impossible.
.
Thus an a-band can end either on a disc or on the boundary of a (a,q,r)-cell. The latter belongs to an r-band and we already know that the diagram contains only a ``small number" of r-bands. Thus if the a disc has a very big perimeter and many of the a-bands starting on the contour of this disc end on boundaries of (a,q,r)-cells, then many of these a-bands must end on the contour of the same r-band. The following lemma shows that it is impossible.
Sketch of the Proof. Indeed, if n>2then there are three a-bands, say,
![]() ,
,
![]() ,
,
![]() starting on p and ending on three different cells
starting on p and ending on three different cells ![]() ,
,
![]() and
and
![]() of
of ![]() .
We can assume that
.
We can assume that ![]() is between
is between ![]() and
and
![]() (see
Figure 13). Consider the minimal subdiagram
(see
Figure 13). Consider the minimal subdiagram ![]() of our diagram
containing a-bands
of our diagram
containing a-bands
![]() ,
the minimal subpath
of the path p containing the starting edges of
,
the minimal subpath
of the path p containing the starting edges of
![]() ,
,
![]() ,
,
![]() ,
and the part of the band
,
and the part of the band ![]() between
between ![]() and
and ![]() Then
Then ![]() has
no k-edges on its contour. Therefore
has
no k-edges on its contour. Therefore ![]() does not contain
discs. Therefore the maximal
q-band
does not contain
discs. Therefore the maximal
q-band ![]() in
in ![]() containing
containing ![]() divides
divides
![]() into two parts (that is if we delete the q-edges
from
into two parts (that is if we delete the q-edges
from ![]() ,
the diagram
,
the diagram ![]() will fall into two pieces). The subpath
of the path p containing the start edges of
will fall into two pieces). The subpath
of the path p containing the start edges of
![]() is
contained in one of these parts since it does not contain
is
contained in one of these parts since it does not contain
![]() -edges. The cells
-edges. The cells ![]() and
and ![]() belong to different parts because
belong to different parts because
![]() cannot intersect
cannot intersect ![]() twice. Since the
twice. Since the
![]() and
and ![]() are connected with the cells on p by a-bands, one of these bands must intersect
are connected with the cells on p by a-bands, one of these bands must intersect ![]() which is impossible (a
q-band cannot cross an a-band).
which is impossible (a
q-band cannot cross an a-band). ![]()
Finally we need to estimate the number and perimeters of B-cells (i.e. cells
corresponding to relations of the group
![]() ). Here we use the following
trick. Suppose that two B-cells are connected by a b-band consisting of (a,b)-commutativity cell. Then we can cut the two B-cells together with the b-band from the
diagram, and replace it by one B-cell and a number of (a,b)-commutativity relations.
This reduces the type of the diagram because the commutativity relations have smaller rank
than B-relations.
Figure 14 shows how this surgery proceeds.
). Here we use the following
trick. Suppose that two B-cells are connected by a b-band consisting of (a,b)-commutativity cell. Then we can cut the two B-cells together with the b-band from the
diagram, and replace it by one B-cell and a number of (a,b)-commutativity relations.
This reduces the type of the diagram because the commutativity relations have smaller rank
than B-relations.
Figure 14 shows how this surgery proceeds.
![]()
![]()
This implies that every b-band starting on the contour of a B-cell must
end either on the boundary of the diagram or on the contour of a
![]() -cell. The number of maximal a-bands in the diagram is
bounded (because the total perimeter of the discs is bounded, and the number
of q-cells is bounded too), and a lemma similar to Lemma 2 shows
that the number of b-bands starting on the contour of the same B-cell
and ending on the contour of the same a-band is at most 2. This leads to
the bound of the number of B-cells and the total perimeter of B-cells.
-cell. The number of maximal a-bands in the diagram is
bounded (because the total perimeter of the discs is bounded, and the number
of q-cells is bounded too), and a lemma similar to Lemma 2 shows
that the number of b-bands starting on the contour of the same B-cell
and ending on the contour of the same a-band is at most 2. This leads to
the bound of the number of B-cells and the total perimeter of B-cells.
Finally we can estimate the areas of words in H relative to the finite presentation of H. Take any word w which is equal to 1 in H. Then there exists a diagram over the infinite presentation of H (with discs and B-cells) with boundary label w. The total perimeter of discs and B-cells is bounded by a polynomial in |w|. Now replace every disc by the van Kampen diagram over the finite presentation of H (as in Fig. 15), and replace each B-cell by the diagram on Fig. 15 consisting of two discs and a relatively small number of other cells. The resulting diagram will be a van Kampen diagram over the finite presentation of H. It is easy to see that if the perimeter of a disc is p then the area is O(T(p)2) where T is the time function of the S-machine. This gives an estimate of the area of w which is polynomially equivalent to T(|w|).