Wolfram's math disproves "intelligent
design"
The math described on this web page is Stephen Wolfram's,
but the subsequent opinions about theology and society are mine.
I am writing this web page because I am
tired of hearing science attacked and undermined by people who do not
understand or respect it.
One formulation of
"intelligent design" can be summarized as follows:
| | (1) |
The world around us is filled with both order and complexity -- "ordered complexity,"
if you will; and |
| |
| | (2) |
such ordered complexity could not have arisen by accident. |
| |
| Therefore |
| |
| | (3) |
there is, or was, some intelligence who designed this world. |
Now, I certainly agree with (1). And although I am not convinced of
(3), I cannot disprove it (see next paragraph). My quarrel is with (2).
If (3) turns out to be true, we may or may not someday
have proof of it. (Some people say we already have
proof, but I mean proof that is strong enough to
convince everyone.)
But if (3) turns out to be false,
we still will never have definitive proof of it.
Indeed,
even if we someday finish filling in all the details
in a scientific explanation of the universe,
so detailed and so supported by evidence that it is
indisputable,
and even if it turns out that god doesn't show
up anywhere in that explanation,
we will still be unable to
rule out the possibility
that some creator built this universe
but -- for reasons known only to him --
intentionally designed it in such a way
as to hide his own part in its creation.
He could have put the fossils
under the mountains, and faked the age
of everything so expertly that he
could fool our carbon-dating
and red-shift measurements.
(Indeed, maybe he created us all
this morning, and gave us fake memories
of what happened yesterday and earlier.)
Some have suggested that he is now sitting in a coffeeshop
somewhere, reading newspaper accounts of
the school board trials, and
chuckling over how he fooled us.
So I am not trying to disprove (3);
I know I can't.
This web page is concerned
only with showing that (2) is not valid reasoning,
and does not constitute a proof of (3).
I assert that statement (2)
is mathematically just plain wrong -- and I assert that
the wrongness of (2) is not merely opinion, but fact. The
people who believe (2) are being rather unimaginative, but in addition
to imagination I can offer evidence.
Stephen Wolfram's book
shows -- with mathematical examples --
how complex systems can arise
from simple ones. I will sketch some of the ideas below.
 A cellular automaton is a sort of self-propelled computer program.
You specify the initial conditions and the transformation rules, and
then you tell it to "go," and the program proceeds to do things on its own.
Probably the best known example of a cellular automaton is
the "Game of Life," devised by mathematician
John Horton Conway in 1970 and popularized by
mathematics journalist Martin Gardner in the same year.
You can see an illustration from that game, to the left
of this paragraph. The program operates on a two-dimensional array
of squares. Each square is either black (alive) or white (dead, or empty),
at each instant of time. The status of cell X at time n+1 is determined
by the status of X and its immediate neighbors at time n.
A cellular automaton is a sort of self-propelled computer program.
You specify the initial conditions and the transformation rules, and
then you tell it to "go," and the program proceeds to do things on its own.
Probably the best known example of a cellular automaton is
the "Game of Life," devised by mathematician
John Horton Conway in 1970 and popularized by
mathematics journalist Martin Gardner in the same year.
You can see an illustration from that game, to the left
of this paragraph. The program operates on a two-dimensional array
of squares. Each square is either black (alive) or white (dead, or empty),
at each instant of time. The status of cell X at time n+1 is determined
by the status of X and its immediate neighbors at time n.
The rules are simple enough that
they could easily be programmed into even the rather rudimentary
computers that were available in 1970. Investigating the patterns
of "Life" became a recreational pastime of many programmers.
Nowadays,
if you're interested in seeing more of this game, you don't have
to be a computer programmer; you can just download one
of the programs that someone else has already written for your
personal computer.

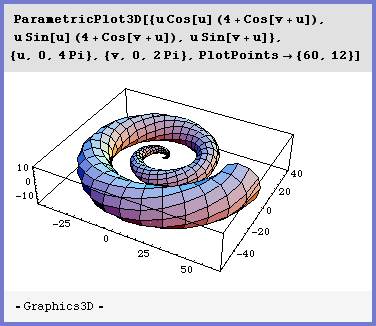 Stephen
Wolfram made himself famous (among scientists,
at least) with his creation of Mathematica, a computer
program widely used by scientists since 1988. (See illustration at right.)
The program
continues to improve with new editions. It (and other programs
like it, though Mathematica is the leader in this genre)
have made a new kind of mathematics possible: Mathematics
has always been theorems and proofs, but now it is also
experiments. With just a few minutes' work, a mathematician
can now generate dozens or hundreds of examples and look at
pictures of the results; this makes it easier to discover
conceptual principles that underlie the examples and are
shared by them.
Stephen
Wolfram made himself famous (among scientists,
at least) with his creation of Mathematica, a computer
program widely used by scientists since 1988. (See illustration at right.)
The program
continues to improve with new editions. It (and other programs
like it, though Mathematica is the leader in this genre)
have made a new kind of mathematics possible: Mathematics
has always been theorems and proofs, but now it is also
experiments. With just a few minutes' work, a mathematician
can now generate dozens or hundreds of examples and look at
pictures of the results; this makes it easier to discover
conceptual principles that underlie the examples and are
shared by them.
But for many years Wolfram also worked on
mathematical research,
using such computer experiments. He learned in 1982
that complexity in mathematical systems can arise from
very simple origins. He investigated this idea extensively
for many years.
He finally published some of
his findings in 2002, in an enormous book titled
A New Kind of Science. It was a science book which received
mixed reviews from the scientific community -- not because there was
anything wrong with Wolfram's science, but because of the slightly
unconventional way that he published it: as a large, popular, expository,
self-published book, rather than as a specialized, arcane article
in a peer-reviewed journal.
Wolfram did not publish the book
for profit -- you can read
the book for free online
if you simply register. If you want a printed copy,
don't bother printing it out yourself --
your costs won't be much less than what Wolfram is charging for a very
nicely bound copy.
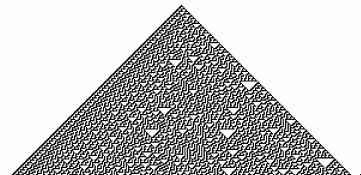 Wolfram studied many examples of simple mathematical systems that
give rise to complexity. Featured prominently
in the book is one class of 256 experiments which might
be termed the simplest possible cellular automata; they are simpler
than the "game of life."
Each of these automata acts on a row (i.e., a one-dimensional array) of
black and white squares, but we get an interesting two-dimensional
picture by stacking the rows -- i.e., the row at time 1, and below
it the row at time 2, and below it the row at time 3, etc.
Wolfram studied many examples of simple mathematical systems that
give rise to complexity. Featured prominently
in the book is one class of 256 experiments which might
be termed the simplest possible cellular automata; they are simpler
than the "game of life."
Each of these automata acts on a row (i.e., a one-dimensional array) of
black and white squares, but we get an interesting two-dimensional
picture by stacking the rows -- i.e., the row at time 1, and below
it the row at time 2, and below it the row at time 3, etc.
Each picture is generated by an extremely simple rule
-- one that could easily
occur "by accident" in nature, as it were -- but many
of the pictures show incredible ordered complexity.
For instance, a small portion of
picture number 30 is shown at the right. You can
see that its right half is very disordered, but some
order is apparent on the left half. And the whole
picture is very complicated; yet it is generated by a very simple rule.
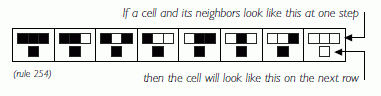 In each picture, the top row has only one black square.
In rows below that, each cell's behavior (black or white)
is determined by the
behavior of the three cells above it
(directly above, diagonally left, and diagonally right).
There are 2x2x2 = 8 possible
behaviors of those three cells:
black-black-black, black-black-white, and so on. For each of those
8 combinations, the rule must specify either a black result or a white result
in the new row.
Thus, to specify a rule, we must specify 8 yes-or-no choices.
The number of rules of this sort is therefore
2x2x2x2x2x2x2x2 = 256.
The book's website includes a very nice one-page summary of this idea, including some pictures that illustrate
rule 30, rule 90, and rule 254.
In each picture, the top row has only one black square.
In rows below that, each cell's behavior (black or white)
is determined by the
behavior of the three cells above it
(directly above, diagonally left, and diagonally right).
There are 2x2x2 = 8 possible
behaviors of those three cells:
black-black-black, black-black-white, and so on. For each of those
8 combinations, the rule must specify either a black result or a white result
in the new row.
Thus, to specify a rule, we must specify 8 yes-or-no choices.
The number of rules of this sort is therefore
2x2x2x2x2x2x2x2 = 256.
The book's website includes a very nice one-page summary of this idea, including some pictures that illustrate
rule 30, rule 90, and rule 254.
 Another way to get complicated pictures from simple rules
is to use points on a plane instead of black and white squares.
Another way to get complicated pictures from simple rules
is to use points on a plane instead of black and white squares.
 Fractals
have been popular among mathematicians since their
study was made possible by modern computers around the
mid-1970's; some of
these immensely complicated pictures are generated by very simple
rules. For instance, the
Mandelbrot set,
shown at right,
consists of the set
of points c in the complex plane for which the iteratively defined sequence
Fractals
have been popular among mathematicians since their
study was made possible by modern computers around the
mid-1970's; some of
these immensely complicated pictures are generated by very simple
rules. For instance, the
Mandelbrot set,
shown at right,
consists of the set
of points c in the complex plane for which the iteratively defined sequence
z0 = 0, zn+1 = zn2 + c
does not tend to infinity. Iterative applications of simple rules produce many amazing fractal
images, and some of them strongly resemble images seen in nature. An example of this is
Barnsley's fern, shown at left.
The works described above are experiments conducted on computers,
but the ideas are mathematical. The certainty of mathematics is greater
than that of any of the other sciences. In a chemistry or physics experiment,
there is always the possibility that the outcome is influenced by some phenomena
that have not yet been observed -- e.g., that our instruments aren't sensitive enough,
or our perception is not unbiased enough. But a problem in mathematics is finite;
a mathematics problem
has only the ingredients that are put into the problem by the mathematician.
There are no hidden influences, and so we can be completely certain of the outcome.
Wolfram's book does mention some of the similarities
between mathematically generated patterns and patterns in nature.
Wolfram also
mentions intelligent design very briefly,
both with regard to complexity
and with regard to purpose.
But for the most part he avoids the controversy. After all, his book is one
of science, not sociology or politics.
 But I will face that controversy right here, because I am tired of hearing
people who understand nothing of science claiming that they have an
equally justifiable explanation of things.
The advocates of intelligent design are simply
wrong when they say that ordered complexity cannot occur by accident.
Wolfram's mathematics shows in examples that
ordered complexity does occur by accident.
But I will face that controversy right here, because I am tired of hearing
people who understand nothing of science claiming that they have an
equally justifiable explanation of things.
The advocates of intelligent design are simply
wrong when they say that ordered complexity cannot occur by accident.
Wolfram's mathematics shows in examples that
ordered complexity does occur by accident.
Let me emphasize that I am not asserting
the nonexistence of God.
If you want to believe in a God, I won't dispute it; I just hope
that ordered complexity isn't the foundation of your belief.
Most of us prefer to believe in whatever is
the simplest explanation
that fits all the facts. Scientists often
call this a principle of science, but most
non-scientists follow this rule too.
However, what is "simplest" is
a somewhat subjective matter.
For instance, what makes an automobile go? It is
"the internal combustion engine" if you have studied
and understand
such things, or if you at least have some respect for
the people who built the car or who know how to repair it.
But it is "magic"
if you have neither that understanding nor that respect.
Most people in our society do respect their
automobile mechanics. I'm
sorry that so many people don't have
the same respect for
biology researchers,
who trained for much longer.
If you want to teach creationism or "intelligent design"
in science classes in
schools, I think you should explain it to students this way:
Some people prefer to believe in creationism or
"intelligent design" because they find that explanation
simpler than the secular view that is prevalent in
the scientific community -- though that preference reflects
their own lack of understanding of the ideas that the
scientific community has produced. One of the goals
of this science class is to explain evolution
so that you do understand it.
Moreover, despite overwhelming evidence (perhaps because they
have not looked at the evidence), some
people continue to believe that the universe cannot be
explained without the presence of a creator. One of the
goals of this science course is to show you that it
can be explained without that additional assumption.
By the way, the Wolfram examples only show complexity
building upward, but biological evolution has other
mechanisms available too, involving the removal of
structures. Don Lindsay, a computer scientist,
has posted a particularly clear
web page explaining some of these mechanisms.
Still another point of confusion may stem from the general
public's poor understanding of probability. (The lottery is a tax
levied on people who do not know math.) I think that most
scientists would agree that relatively few planets are suitable
for the origination of life -- i.e., if you pick a planet at
random, there's very little chance that it will be a planet where
life can develop. However, that does not mean that our
being on such a planet is unlikely. To understand the question,
you have to turn it around and ask it the other way. Given
that we did wake up one day (or one millenium) and start asking
questions, what are the odds that we did it on one of the
few planets capable of sustaining life? Very high, obviously.
Or here is still another way to put the question: There are
billions of planets in the universe. No two are identical, but
we could classify them into certain "types" according to whether
they have similar chemical compositions, axial tilts, distance
from their parent stars, and so on. Is there a certain "type"
of planet on which life is highly likely to evolve?
Most astrobiologists would say yes. If you're interested
in this sort of question, you might want to look at Wiki's
discussion of the
Drake equation.
Why does it matter? What is the harm in introducing
a bit of theology in a science class?
Well, science and theology operate on entirely different
principles, and belong in different places.
-
The "scientific method"
operates on these principles: Question everything
and everyone, even your teachers. A document's
great age does not make it authoritative;
there is no authority
except repeatable experimental evidence and pure reason.
Moreover,
one must constantly be on guard against biases
(accidental or otherwise) in the
experiments or implicit assumptions in the reasoning.
No answer is ever final -- an established tradition
can be overthrown instantly
if its experimental evidence is shown
to have overlooked something or to be faulty in
some other respect -- but until such an overthrow,
proper respect must be given to
"theories" that are supported by overwhelming evidence.
-
Theology, on the other hand, operates on rather
different principles. I'm not sure what they are --
I'm no expert on theology -- but authority and tradition
appear to play bigger roles, and experiment plays a
much smaller role, as far as I can see.
If you label theology as "science" and teach it as such
in a science classroom, you are simply lying. Some students
will be fooled, and will end up with a rather poor understanding
of the scientific method. (Perhaps that is the goal
of some creationists?)
Other students will not be fooled, and
will end up disrespecting the school system.
I find both those outcomes
to be highly undesirable.
In addition to purely philosophical reasons, there are also
practical reasons.
As historian Edward J. Larson has
explained,
the evolutionary viewpoint has been confirmed by its measurable productivity:
Its insights have led to discoveries in medicine, biotechnology, etc. -- i.e., it
has improved our lives. Its lessons should not be denied to our
students, nor obscured by unrelated notions.
an essay by Eric Schechter,
version of 9 April 2006.
 A cellular automaton is a sort of self-propelled computer program.
You specify the initial conditions and the transformation rules, and
then you tell it to "go," and the program proceeds to do things on its own.
Probably the best known example of a cellular automaton is
the "Game of Life," devised by mathematician
John Horton Conway in 1970 and popularized by
mathematics journalist Martin Gardner in the same year.
You can see an illustration from that game, to the left
of this paragraph. The program operates on a two-dimensional array
of squares. Each square is either black (alive) or white (dead, or empty),
at each instant of time. The status of cell X at time
A cellular automaton is a sort of self-propelled computer program.
You specify the initial conditions and the transformation rules, and
then you tell it to "go," and the program proceeds to do things on its own.
Probably the best known example of a cellular automaton is
the "Game of Life," devised by mathematician
John Horton Conway in 1970 and popularized by
mathematics journalist Martin Gardner in the same year.
You can see an illustration from that game, to the left
of this paragraph. The program operates on a two-dimensional array
of squares. Each square is either black (alive) or white (dead, or empty),
at each instant of time. The status of cell X at time 

 Wolfram studied many examples of simple mathematical systems that
give rise to complexity. Featured prominently
in the book is one class of 256 experiments which might
be termed the simplest possible cellular automata; they are simpler
than the "game of life."
Each of these automata acts on a row (i.e., a one-dimensional array) of
black and white squares, but we get an interesting two-dimensional
picture by stacking the rows -- i.e., the row at time 1, and below
it the row at time 2, and below it the row at time 3, etc.
Wolfram studied many examples of simple mathematical systems that
give rise to complexity. Featured prominently
in the book is one class of 256 experiments which might
be termed the simplest possible cellular automata; they are simpler
than the "game of life."
Each of these automata acts on a row (i.e., a one-dimensional array) of
black and white squares, but we get an interesting two-dimensional
picture by stacking the rows -- i.e., the row at time 1, and below
it the row at time 2, and below it the row at time 3, etc.
 In each picture, the top row has only one black square.
In rows below that, each cell's behavior (black or white)
is determined by the
behavior of the three cells above it
(directly above, diagonally left, and diagonally right).
There are
In each picture, the top row has only one black square.
In rows below that, each cell's behavior (black or white)
is determined by the
behavior of the three cells above it
(directly above, diagonally left, and diagonally right).
There are  Another way to get complicated pictures from simple rules
is to use points on a plane instead of black and white squares.
Another way to get complicated pictures from simple rules
is to use points on a plane instead of black and white squares.

 But I will face that controversy right here, because I am tired of hearing
people who understand nothing of science claiming that they have an
equally justifiable explanation of things.
The advocates of intelligent design are simply
wrong when they say that ordered complexity cannot occur by accident.
Wolfram's mathematics shows in examples that
ordered complexity does occur by accident.
But I will face that controversy right here, because I am tired of hearing
people who understand nothing of science claiming that they have an
equally justifiable explanation of things.
The advocates of intelligent design are simply
wrong when they say that ordered complexity cannot occur by accident.
Wolfram's mathematics shows in examples that
ordered complexity does occur by accident.