Linear Transformations From Rn to Rm
Linear Transformations From Rn to Rm
 Linear Transformations From Rn to Rm
Linear Transformations From Rn to RmThere is a yet another way to look at systems of linear equations. Suppose that we want to find all solutions of the following system of linear equations
where A is an m by n matrix of coefficients and b is the column of right
sides. For every n-vector v we can get an m-vector Av.
Our goal is to find
all n-vectors v such that this m-vector is b.
Thus we have a function which takes any vector
v from Rn to the vector Av from Rm and our goal is to find all values
of the argument of this function for which the function has a particular
value.
A function from
Rn to Rm which takes every n-vector v to the m-vector
Av where A is a m by n matrix, is called a linear transformation.
The matrix A is called the standard matrix
of this transformation. If n=m then the transformation
is called a
linear operator of the vector space Rn.
Notice that by the definition the linear transformation with a standard matrix A takes every vector
from Rn to the vector
from Rm where A(i,j) are the entries of A.
Conversely, every transformation from Rn to Rm given by a formula of this
kind is a linear transformation and the coefficients A(i,j) form the standard
matrix of this transformation.
Examples. 1. Consider the transformation of R2 which takes
each vector (a,b) to the opposite vector (-a,-b). This is a linear operator
with standard matrix
| [ -1 | 0 ] |
| [ 0 | -1 ] |
2. More generally, the dilation operator is the linear operator from Rn to Rn which takes every vector
to
where k is a constant.
3. If we take a vector (x,y) in R2 and reflect it about the x-axis, we get vector (x,-y). Clearly, this reflection is a linear operator. Its standard matrix is
| [ 1 | 0 ] |
| [ 0 | -1 ] |
4. If we project a vector (x,y) on the x-axis, we get vector (x,0). This projection is also a linear operator. Its standard matrix is
| [ 1 | 0 ] |
| [ 0 | 0 ] |
5. If we rotate a vector (x,y) through 90 degrees counterclockwise, we get vector (-y, x). This rotation is a linear operator with standard matrix
| [ 0 | -1 ] |
| [ 1 | 0 ] |
 A characterization of linear transformations
A characterization of linear transformations
We shall prove that reflections about arbitrary lines, projections on
arbitrary axes, and rotations through arbitrary angles in R2 are linear
operators. In order to do this we need the following simple
characterization of linear transformations from Rn to Rn.
 Theorem. A function T from Rn to Rm is
a linear transformation if and only if it satisfies the following two
properties:
Theorem. A function T from Rn to Rm is
a linear transformation if and only if it satisfies the following two
properties:
This proof shows that if T is a linear transformation, Vi (I=1,...,n)
is the vector with I-th coordinate 1 and other coordinates 0, then
T(Vi) is the I-th column in the standard matrix of T.
This provides us with
a way to find the standard matrix of a linear transformation.
Notice that in R3, vectors V1, V2, V3 are the basic vectors i, j, k. So we shall call Vi the
basic vectors in Rn. We shall give a general definition of bases
in Rn and other vector spaces later.
As a corollary of the characterization of linear transformations from
Rm to Rn we can deduce the following statement.
 Corollary. Every linear transformation T from Rm to Rn
takes 0 of Rm to 0 of Rn.
Corollary. Every linear transformation T from Rm to Rn
takes 0 of Rm to 0 of Rn.
Indeed, take k=0 and an arbitrary vector A then
Here we used the second condition of the characterization.
 Linear operators in R2
Linear operators in R2
Example 1. Projection on an arbitrary line in R2.
Let L be an arbitrary line in R2. Let TL be the transformation of R2 which
takes every 2-vector to its projection on L. It is clear that
the projection of the sum of two vectors is the sum of the projections of these
vectors. If we multiply a vector by a scalar then its projection will also
be multiplied by this scalar. Thus by the characterization of linear transformations, TL is a linear operator on R2.
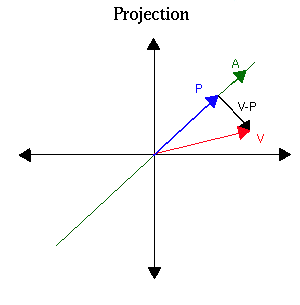
From this, we can deduce that
So
Therefore the standard matrix of the projection is
| 1/(k2+1) | [ 1 | k ] |
| [ k | k2 ] |
Example 2. Reflection about an arbitrary line.
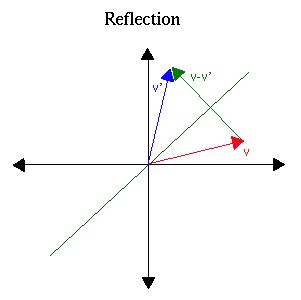
This gives us the standard matrix of the reflection:
| 1/(k2+1) | [ 1-k2 | 2k ] |
| [ 2k | k2-1 ] |
Example 3. Rotation through angle a
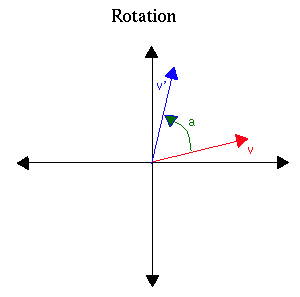
| [ cos(a) | -sin(a) ] |
| [ sin(a) | cos(a) ] |
Notice that the rotation clockwise by angle a has the following matrix:
| [ cos(a) | sin (a) ] |
| [ -sin(a) | cos(a) ] |
because it is equal to the rotation
counterclockwise through the angle -a.
 Operations on linear transformations
Operations on linear transformations
Suppose that T is a linear transformation from Rm to Rn with standard
matrix A and S is a
linear transformation from Rn to Rk with standard matrix B. Then we can
compose or multiply
these two transformations and create a new
transformation ST which takes vectors from Rm to Rk. This transformation
first applies T and then S. Not any two transformations can be multiplied:
the transformation S must start where T ends. But any two linear operators
in Rn (that is linear transformations from Rn to Rn) can be multiplied.
Notice that if v is a vector in Rn then
by the definition of the
standard matrix of a linear transformation. Then
Thus the product ST is a linear transformation and the standard matrix ST is the product of standard matrices BA.
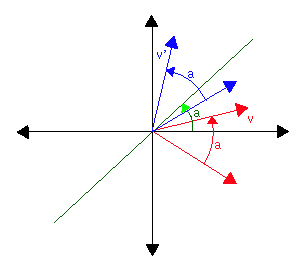
Example 1. Suppose that T and S are rotations in R2,
T rotates through angle a and S rotates through angle b (all rotations
are counterclockwise). Then
ST is of course the rotation through angle a+b. The standard matrix
of T is
| [ cos(a) | -sin(a) ] |
| [ sin(a) | cos(a) ] |
| [ cos(b) | -sin(b) ] |
| [ sin(b) | cos(b) ] |
| [ cos(a)cos(b)-sin(a)sin(b) | -cos(a)sin(b)-sin(a)cos(b) ] |
| [ cos(a)sin(b)+sin(a)cos(b) | cos(a)cos(b)-sin(a)sin(b) ] |
| [ cos(a+b) | -sin(a+b) ] |
| [ sin(a+b) | cos(a+b) ] |
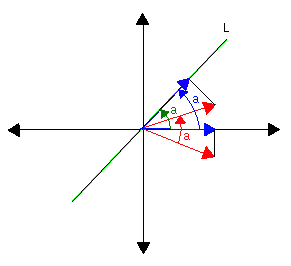
Thus we could find the standard matrix of the reflection about the line L
by multiplying the standard matrices of these three transformations.
Similarly, the projection on L can be decomposed into a product of three
operators:
We can also multiply a linear transformation by a scalar. If k is a number
and T is a linear transformation from Rm to Rn then kT is a function from
Rm to Rn which takes every vector V from Rm to kT(V). It is
easy to see that the standard matrix of kT is kA.
Summarizing the properties of linear transformations from Rm to Rn that
we have obtained so far, we can formulate the following theorem.
 Theorem. 1. The product ST of
a linear transformation T from Rm to Rn and a linear transformation S
from Rn to Rk is a linear transformation from Rm to Rk
and the standard matrix
of ST is equal to the product of standard matrices of S and T.
Theorem. 1. The product ST of
a linear transformation T from Rm to Rn and a linear transformation S
from Rn to Rk is a linear transformation from Rm to Rk
and the standard matrix
of ST is equal to the product of standard matrices of S and T.
2. If T and S are linear transformations from Rm to Rn then T+S is
again a
linear transformation from Rm to Rn and the standard matrix of
this transformation is equal to the sum of standard matrices of T and S.
3. If T is a linear transformation from Rm to Rn and k is a scalar then
kT is again a
linear transformation from Rm to Rn and the standard matrix of
this transformation is equal to k times the standard matrix of T.
By definition, the identity
function from Rn to Rn
is the function which takes every vector to itself. It is clear that the identity function is a linear operator whose standard matrix is the identity matrix.
Let us denote the identity operator by Id.
A linear operator T in Rn is called invertible if there exists another linear operator S in Rn such that TS=ST=Id. In this case S is called the inverse of T. By definition S undoes what T does, that is if T takes V to W then S must take W to V (otherwise ST would not be the identity operator). If A is the standard matrix of T and B is the standard matrix of S then ST has standard matrix BA. So if S is the inverse of T then BA=I. Conversely, if BA=I then the linear operator S with standard matrix B is the inverse of T because ST is the linear operator whose standard matrix is I. Thus we can conclude that the following statement is true.
 Theorem. A linear operator T in Rn
is invertible if and only if its standard matrix is invertible. If A is the
standard matrix of T then A-1 is the standard matrix of T-1.
Theorem. A linear operator T in Rn
is invertible if and only if its standard matrix is invertible. If A is the
standard matrix of T then A-1 is the standard matrix of T-1.
Example 1. The reflection about a line in R2 is invertible
and the inverse of a reflection is the reflection itself (indeed, if we apply the reflection to a vector twice, we do not change the vector).
Example 2. The rotation through angle a is invertible and the inverse is the rotation through angle -a.
Example 3. The projection on a line in R2 is not invertible because there are many vectors taken by the projection to the same vector, so we cannot uniquely reconstruct a vector by its image under the projection.
Our next goal is to consider properties of invertible linear operators.
First let us recall some properties of invertible maps (functions). Let
T be a map from set X into set Y. We say that T is
injective or one to one
if T maps different elements to different elements, that is if
T(u)=T(v) then necessarily u=v. We
call T surjective
or onto if every element in Y is an image of some element in
X that is for every y in Y there exists an x in X such that T(x)=y.
A function T from X to X is called invertible if
there exists another function S from X to X such that TS=ST=Id, the identity
function (that is if T takes x to y then S must take y to x). It is easy to see
that T is invertible if and only if it is injective and surjective.
There exist functions which are non-injective and non-surjective
(the function T(x)=x2 from R to R), non-injective and surjective (say,
T(x)=x3-x
from R to R), injective and non-surjective (say, T(x)=arctan(x) from R to R),
injective
and surjective (any invertible function, say T(x)=x3 from R to R).
Thus the following theorem about linear operators is very surprising.
 Theorem. For every linear operator T in Rn with standard matrix A the
following conditions are equivalent:
Theorem. For every linear operator T in Rn with standard matrix A the
following conditions are equivalent:

 Linear transformations of arbitrary vector spaces
Linear transformations of arbitrary vector spacesLet V and W be arbitrary vector spaces. A map T from V to W is called a linear transformation if
In
the particular case when V=W, T is called a linear operator in V.
We have seen (see the characterization
of linear transformations from Rm to Rn) that linear transformations from
Rm to Rn are precisely the maps which satisfy these conditions. Therefore in
the case of vector spaces of n-vectors this definition is equivalent to the
original definition. Other vector spaces give us more examples of natural
linear transformations.
Positive examples.1. Let V be the set of all polynomials in one
variable. We shall see later that V is a vector space with the natural
addition and scalar multiplication (it is not difficult to show it directly).
The map which takes each polynomial to its derivative is a linear
operator in V as easily follows from the properties of derivative:
2. Let C[0,1] be the vector space of all continuous functions on the interval
[0,1]. Then the map which takes every function S(x) from C[0,1] to the
function h(x) which is equal to the integral from 0 to x of S(t) is a linear
operator in C[0,1] as follows from the properties of integrals.
3. The map from C[0,1] to R which takes every function S(x) to the number
S(1/3) is a linear transformation (1/3 can be replaced by any number between
0
and 1):
4. The map from the vector space of all complex numbers C to itself
which
takes every complex number a+bi to its imaginary part bi is a linear operator
(check!).
5. The map from the vector space of all n by n matrices (n is fixed) to
R which takes every matrix A to its (1,1)-entry A(1,1) is a linear
transformation (check!).
6. The map from the vector space of all n by n matrices to R which takes
every matrix A to its trace trace(A) is a linear transformation (check!).
7. The map from an arbitrary vector space V to an arbitrary vector space W
which takes every vector v from V to 0 is a linear transformation (check!).
This transformation is called the null
transformation
8. The map from an arbitrary vector space V to V which takes every vector to itself (the identity map) is a linear operator (check!). It is called the identity operator, denoted I.
Negative examples. 1. The map T from which takes every
function
S(x) from C[0,1] to the function S(x)+1 is not a linear transformation
because if we take k=0, S(x)=x then the image of kT(x) (=0) is the constant
function 1 and k times the image of T(x) is the constant function 0. So the
second property of linear transformations does not hold.
2. The map T from the vector space of complex numbers C to R which takes
every complex number a+bi to its norm sqrt(a2+b2) is not a linear
transformation because if we take A=3 and B=4i then T(A+B)=||3+4i||=5
and T(A)+T(B)=3+4=7, so T(A+B) is not equal to T(A)+T(B), so the first property
of linear transformations does not hold.
The following theorem contains some important properties of linear
transformations (compare with the corollary from the
characterization T linear transformations from Rm to Rn and
the theorem about products, sums and scalar
multiples of linear transformations).
 Theorem. 1. If T is a linear transformation
from V to W then T(0)=0.
Theorem. 1. If T is a linear transformation
from V to W then T(0)=0.
2. If T is a linear transformation from V to W and S is a linear
transformation from W to Y (V, W, Y are vector spaces)
then the product (composition) ST is a linear
transformation from V to Y.
3. If T and S are linear transformations from V to W (V and W are vector
spaces) then the sum T+S
which takes every vector A in V to the sum
T(A)+S(A) in W is again a linear transformation from V to W.
4. If T is a linear transformation from V to W and k is a scalar then the
map kT which takes every vector A in V to k times T(A) is again a linear
transformation from V to W.
 The proof is left as an exercise.
The proof is left as an exercise.
Some properties of linear transformations, which hold for linear
transformations from Rm to Rn, do not hold for arbitrary vector spaces.
For example let P be the vector space of all polynomials.
Let T be the
linear operator which takes every polynomial to its derivative. Then T is
surjective because every polynomial is a derivative of some other polynomial
(anti-derivatives of a polynomial are polynomials). But T is not injective
because the images of x2 and x2+1 are the same (2x).
Recall that for linear transformations from Rm to Rn injectiveness and
surjectiveness are equivalent.
Notice that since the operator T is not injective, it cannot have an
inverse. But let S be the operator on the same space
which takes every polynomial to its anti-derivative int(p(t), t=0..x).
Then for every polynomial p we have: TS(p)=p (the derivative of the
anti-derivative of a function is the function itself). Thus TS=I. On the other
hand ST is not equal to I, for, say if p=x+1 then T(p)=1, ST(p)=x, so ST(p)
is not equal to p.
For linear operators in Rm, this cannot happen. Indeed, if TS=I
then the product of standard matrices of T and S is I.
So the standard matrix
A of T is invertible, and the standard matrix B of S is
the inverse of A. Hence S is the inverse of T and ST=I.
 The proof in the last paragraph does not have references to the results
that we used. Find these references!
The proof in the last paragraph does not have references to the results
that we used. Find these references!