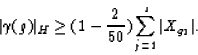Here we present the main ideas of the proofs of results from [30] (see Section 1.3).
If G is a subgroup of a group H with a finite set of generators
![]() then the function
then the function
![]() on G evidently
satisfies conditions (D1)-(D3) from Theorem 8.
For instance condition (D3) holds because the
number of all words of length at most k in the alphabet B grows
exponentially as
on G evidently
satisfies conditions (D1)-(D3) from Theorem 8.
For instance condition (D3) holds because the
number of all words of length at most k in the alphabet B grows
exponentially as
![]() .
.
To prove that every function
![]() satisfying conditions (D1)-(D3)
can be realized as the length function of G inside a finitely generated
group H, we start with a presentation G = FG/N, where FG is a free
group with the basis
satisfying conditions (D1)-(D3)
can be realized as the length function of G inside a finitely generated
group H, we start with a presentation G = FG/N, where FG is a free
group with the basis
![]() and N is the
kernel of homomorphism
and N is the
kernel of homomorphism
![]() .
.
Then we construct an embedding
![]() of FG into the
2-generated free group
F=F2=F(b1,b2), such that the image
of FG into the
2-generated free group
F=F2=F(b1,b2), such that the image
![]() is freely generated by Xg,
is freely generated by Xg,
![]() and the words Xgare very ``independent" in the sense described below.
and the words Xgare very ``independent" in the sense described below.
The group H is equal to the quotient F/L, where L is the normal
closure of ![]() in F.
in F.
Notice that whatever homomorphism ![]() we choose, it induces a
homomorphism
we choose, it induces a
homomorphism
![]() .
To make this homomorphism injective,
we need the following property:
.
To make this homomorphism injective,
we need the following property:
(*) For any normal subgroup
![]() there is a
normal subgroup
there is a
normal subgroup
![]() such that
such that
![]() .
.
The fact that free groups and more generally every non-elementary hyperbolic group has plenty of infinitely generated free subgroups with property (*) is interesting in its own right, it was the key ingredient in Olshanskii's proof from [29] of the fact that every non-elementary hyperbolic group is SQ-universal.
It turns out that we can make ![]() satisfy condition (*) by choosing
reduced words Xg with the following small cancellation condition:
satisfy condition (*) by choosing
reduced words Xg with the following small cancellation condition:
(**) If Y is a subword of a word Xg and
![]() then Y occurs in Xg as a subword only once, and Y occurs neither
in Xg-1 nor in
then Y occurs in Xg as a subword only once, and Y occurs neither
in Xg-1 nor in
![]() for
for ![]() .
.
It is relatively easy to construct an infinite set of words
Xg in the alphabet
![]() which satisfies
the (**)-condition and has exponential growth, that is the number of different words Xgof length k grows exponentially as
which satisfies
the (**)-condition and has exponential growth, that is the number of different words Xgof length k grows exponentially as
![]() .
.
Since by condition (D3) the number of elements ![]() with
with
![]() does not exceed
ck for some constant c, we can choose
the set
does not exceed
ck for some constant c, we can choose
the set ![]() in such a way that
in such a way that
We need to show that the embedding
![]() is quasi-isometric. For this we take any element Xg of
is quasi-isometric. For this we take any element Xg of ![]() and consider the shortest word W in the alphabet
and consider the shortest word W in the alphabet
![]() representing Xg in H. The group H is given by the presentation consisting of all relations of the form
Xg1Xg2...Xgn=1 where
g1g2...gn=1 in G.
representing Xg in H. The group H is given by the presentation consisting of all relations of the form
Xg1Xg2...Xgn=1 where
g1g2...gn=1 in G.
Since Xg=W modulo this presentation, we can consider the corresponding van Kampen diagram ![]() with boundary label XgW-1. We can assume that the number of cells in
with boundary label XgW-1. We can assume that the number of cells in ![]() is minimal
among all such diagrams.
is minimal
among all such diagrams.
The condition (**) implies the following property of van Kampen diagrams over the
presentation of H. Let ![]() and
and ![]() be cells in a diagram
be cells in a diagram ![]() having a common edge. Then either any common arc p of the boundaries
having a common edge. Then either any common arc p of the boundaries
![]() and
and
![]() is short compared to the perimeters
P1, P2 of the cells (say,
is short compared to the perimeters
P1, P2 of the cells (say,
![]() ), or a
subdiagram consisting of
), or a
subdiagram consisting of ![]() and
and ![]() ,
has also a boundary label of
the form
,
has also a boundary label of
the form
![]() ,
i.e. the subdiagram can be replaced
by one cell. The latter option cannot occur in
,
i.e. the subdiagram can be replaced
by one cell. The latter option cannot occur in ![]() because of the
minimality of the diagram
because of the
minimality of the diagram ![]() .
Thus
.
Thus ![]() satisfies a small
cancellation condition [25].
satisfies a small
cancellation condition [25].
This in turn allows us to prove that the word W is freely equal to a
product
![]() for some
for some ![]() with
with
![]() (see [30] for details). Further,
since the cancellations in such a product are small,
(see [30] for details). Further,
since the cancellations in such a product are small,